Metrictank Data Distribution: The Quest for the Best Hashing Method
In this blog post, we will discuss the experiments we did to find the best hashing method for Metrictank data distribution.
Metrictank Clustering
Running a Metrictank cluster is easy: Every member of the cluster only needs to know the IP or hostname of at least one other cluster peer to talk to (set in the metrictank.ini config file [cluster] section or in the environment variable MT_CLUSTER_PEERS), and they will then start gossiping peer status and form a cluster.
Any Metrictank instance can serve reads for data residing anywhere in the cluster. A Metrictank instance is aware of all other cluster peers (through gossip), maintains health information on all cluster peers, and fans out any index or data requests to other peers to cover all shards in the cluster.
Each Metrictank instance is assigned one or more partition IDs (32-bit integer). Each metric is also assigned a partition ID. All data with a given partition ID will be sent to the Metrictank instances with the same partition ID. Splitting the data in partitions distributes reading and writing data across the instances. Additionally, multiple Metrictank instances can be assigned the same partitions, thus making Metrictank resilient to the failure of instances and faster to serve read queries for data in a single partition.
Distributing Data: Criteria for Success
Partition assignment happens by hashing the metric metadata.
A good hashing function satisfies the following criteria:
Distribution performance: Metrics must be as evenly distributed across partitions as possible in order to spread the CPU and memory load evenly across computers.
Computational performance. Since we need to compute the partition ID for every piece of data coming in, it cannot be too costly.
Existence of a robust, supported implementation in Go.
Historically, we simply used Sarama’s built-in partitioner, which hashes a []byte key with Fnv-1a (32bit) and then does a modulo of the number of partitions on the resulting number. As we needed to refactor our partitioning, it was time to investigate if we could do better.
In particular, we know the Booking.com Graphite team has reported promising outcomes after adopting jump hash, so we wanted to see if we would have a similar experience. And since jumphash requires a uint64 input (not an arbitrary byte slice), we were curious to find out what’s the best function to preprocess the input to massage it into a uint64 input for go-jump.
Partitioning Function
Conceptually, the partitioning function can be thought of as taking a byte slice input and returning a 32-bit integer, the partitionID. For performance, however, hashing functions in Go expose an io.Writer interface such that you can write directly into them multiple times (you can write multiple fields, which should affect the final hash) without allocation overhead.
The user can choose which attributes of each metric determines the partition ID it will be assigned to. Metrictank supports three possible inputs to the partitioning function.
| Partitioning Input | Type |
|---|---|
| Organization ID | unsigned 32-bit integer (hashed in little endian memory order) |
| Metric name | string |
| Metric name and sorted list of tags | string + slice of strings |
Comparison of Partitioning Functions
As stated before, we had a specific interest in the jump hash function described in 2014 by John Lamping and Eric Veach. Jump needs a uint64 input, not a byte slice. To massage our data into uint64 outputs we tried putting these hash functions in front of jump:
The Fowler–Noll–Vo (FNV) hash function described in 1991 by Glenn Fowler, Landon Curt Noll, and Kiem-Phong Vo.
The SipHash function described in 2012 by Jean-Philippe Aumasson and Daniel J. Bernstein.
The xxHash function described in 2014 by Yann Collet.
The MetroHash function described in 2015 by J. Andrew Rogers.
The “sum” function. For fun, we implemented our own preprocessor, which iterates over a byte slice in groups of 8 bytes, and adds the 8 bytes to the uint64. We were curious to see how this simplistic approach would fare against the true hashing functions. Note that it was not implemented optimally in terms of memory allocations.
We tested and compared 6 partitioning functions and for each computed:
Time spent computing 1 partition ID (averaged over at least 5,000,000 iterations).
Amount of memory allocation computing 1 partition.
| Partitioning Function | Algorithm | Duration | Memory Allocations |
|---|---|---|---|
| FNV-1a + modulo | 32-bit FNV-1a modulo number of partitions (our baseline based on Sarama) | 205 ns | 0 bytes |
| FNV-1a + jump | 64-bit FNV-1a jump hash over number of partitions | 286 ns | 0 bytes |
| sum + jump | sum of all slices of 8 bytes jump hash over number of partitions | 271ns | 210 bytes |
| MetroHash + jump | 64-bit MetroHash jump hash over number of partitions | 101 ns | 0 bytes |
| SipHash-2-4 + jump | 64-bit SipHash-2-4 jump hash over number of partitions | 145 ns | 0 bytes |
| xxHash + jump | 64-bit xxHash jump hash over number of partitions | 99 ns | 0 bytes |
Fun fact: jump hash turned out to be ridiculously fast. So fast, in fact, that we could only properly benchmark it with about a hundred inputs.
As soon as we tried to increase the number of input metrics (all allocated and initialized in advance, ready to go in an array), the benchmark would noticeably slow down due to CPU cache misses. This made it pretty clear go-jump itself would never become a worry.
We then tested these functions on 3 production datasets of sizes ranging from half a million to millions of items, testing with 32 and 128 partitions, and computing each time:
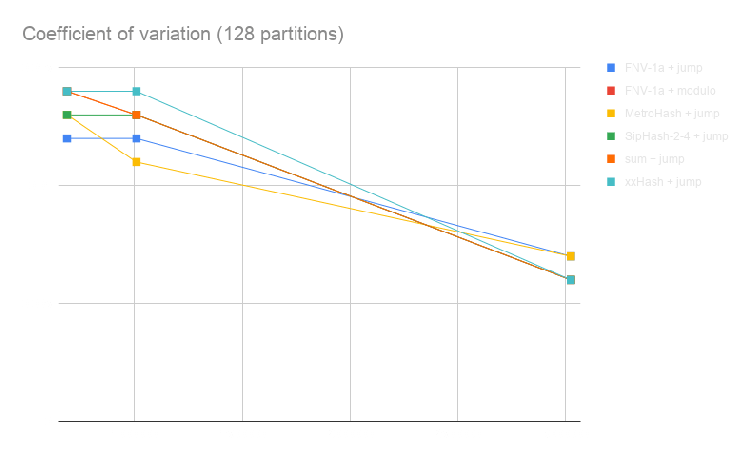
The coefficient of variation – which is the ratio of the standard deviation to the mean (an excellent measure of variation!) – of the number of metrics per partition.
The percentage difference between the minimum number of metrics in a partition and the maximum number of metrics in a partition.
For both criteria, a lower value means a more even distribution of the data across partitions.
We plotted the results for 128 partitions only because they were very similar for 32 partitions:
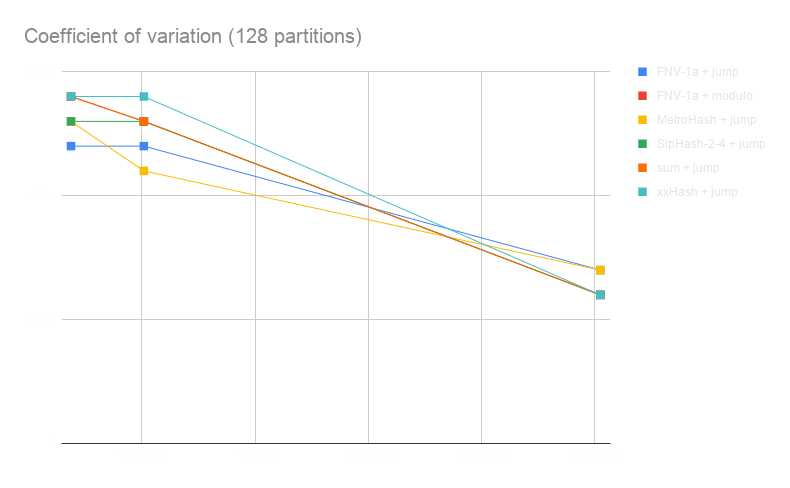
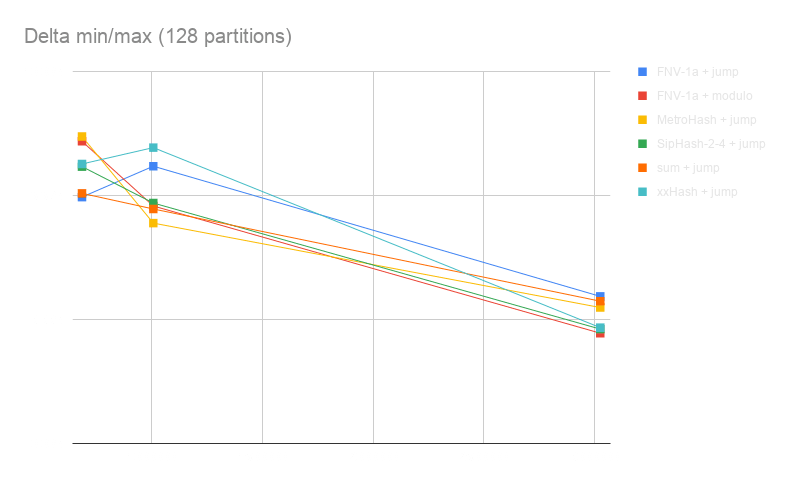
All functions behave quite similarly; however, sum + jump and FNV-1a + jump are much more costly on CPU.
xxHash + jump is very competitive on both criteria when the amount of data increases and is cheaper on CPU than all the other functions.
Conclusion
Until August 2019 Metrictank was using the Sarama hasher (FNV-1a + modulo) exclusively. Given the results from our experiments, we added xxHash + jump and made it the default for any Metrictank with tags support enabled, thus giving us a better data distribution on large clusters.
As we already mentioned, jump hash is ridiculously fast. Combined with xxHash, which is also very optimized, we could hash 10 million metrics per second on a single core, if it weren’t for the rest of the work that needs to be done (encoding/decoding of data, publishing to Kafka, etc.). If hashing ever becomes the bottleneck, we will be very pleased because it means that we were able to extremely optimize the rest of our code.
Another improvement we were able to make after implementing our own partitioner is we no longer publish keys in our Kafka messages. We were only using the keys to generate partitions. This gave us another nice reduction in bandwidth and disk space usage as well!